단순선형회귀를 모르신다면, 아래의 블로깅을 한번 보시는 것을 추천드립니다.
(https://value-error.tistory.com/25)
단순선형회귀( Simple-Regression )
단순선형회귀란 종속변수를 하나의 독립변수로 예측하는 것을 말합니다. 즉 기상청이 풍향 한가지로, 강수 확률을 예측하는 것과 같습니다. 왜 풍향만 보냐고 물어보실 수 있습니다. 단순선형
value-error.tistory.com
다중선형회귀란
- 여러 개의 독립변수(x)를 가지고 종속변수(y)를 예측하기 위한 회귀 모형입니다.
다중선형회귀의 구성
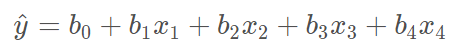
- b1 b2.. 를 편 회귀 계수(Partial regression coefficient)라고 합니다.
- 계수를 통해 설명변수 x1이 종속변수에 대한 영향력을 나타냅니다.
- 즉 독립변수들이 설명변수에 얼마나 영향을 주는지 알 수 있게 해 주며, 이를 통해 예측을 할 수 있게 합니다.
- 단순회귀와 마찬가지로 계수는 최소제곱법를 통해 편미분하여 계수를 추정합니다.
다중선형회귀분석 시 유의할 점
- 독립변수(설명변수)들끼리의 상관관계가 높으면 다중공선성 문제
다중 공선성( multicollinearity )
- 다중 공선성이란, 사용해야 될 독립변수들끼리 서로 밀접한 상관관계가 있어서 다중선형회귀모델에서 각각의 요인들의 효과를 파악하기 어려워지는 것을 말합니다.
- 문제는 단순선형회귀분석 일 때는 중요한 변수로 나타났지만, 다양한 변수들과 함께 적용되는 다중선형회귀분석을 할 때는 유의하지 않게 나온다 것입니다.
- 그래서 다중공성성이 있는 변수들을 회귀모형에 그냥 집어넣게 되면, 추정된 편 회귀 계수의 신뢰성이 떨어질 수 있습니다.
다중 공선성의 해결책
- 다중공선성에 가장 큰 영향을 끼치는 설명변수를 회귀 모델에서 제거하는 것입니다.
- 해당 변수들의 합이나 평균들을 구해서 새로운 변수를 만들어 사용하는 방법이 있습니다
- 그러나 회귀 모형에서 반드시 포함되어야 하는 독립변수를 제거하면 안 됩니다.
파이썬의 scikit-learn으로 다중회귀분석 해보기
예제 데이터 : https://www.kaggle.com/c/house-prices-advanced-regression-techniques/overview
House Prices - Advanced Regression Techniques | Kaggle
www.kaggle.com
import pandas as pd
# 로컬파일 내 혹은 구글드라이브 등에 저장된 house prices 데이터를 가져옵니다.
df = pd.read_csv('파일경로/house-prices/house_prices_train.csv')
## train/test 나누기
train = df.sample(frac=0.7,random_state=1)
test = df.drop(train.index)
# 다중회귀분석 모델 학습을 위한 특성
columns = ['feature1',
'feature2'] # 속성 두개 이상
X_train = train[columns]
X_test = test[columns]
# 모델 fit, 훈련 에러 확인
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
mae = mean_absolute_error(y_train, y_pred)
print(f'훈련 에러: {mae:.2f}')
# 테스트 데이터 에러 확인
y_pred = model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)
print(f'테스트 에러: {mae:.2f}')회귀모델을 평가하는 평가지표들( evaluation metrics )


MSE
- MSE는 Mean Squared Error이라고 하며, 실제 값과 예측값의 차이를 제곱하여 평균 낸 것입니다.
- SSE와 유사하지만, 오차의 자유도(1/n)로 나누어, 평균을 구하는 것이 MAE입니다.
- 나누어 주지 않는다면 데이터 자체가 많은 수록 단순히 커지기 때문에, 오차가 커지므로 자유도로 나눔으로 써, 보정된 평균오차를 모형의 에러 수준으로 판단하게 되는 것입니다.
- 손실함수로 사용 됩니다.


MAE
- MAE는 Mean Absolute Error이라고 하며, 실제값과 예측값의 차이를 절댓값으로 변환하여 평균한 것입니다.
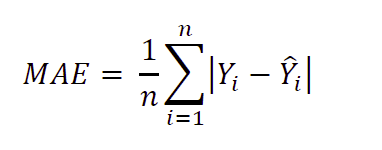
RMSE
- RMSE는 MSE값이 오류의 제곱을 구하기 때문에 실제 오류 평균값보다 더 커지는 성질이 있어, MSE에 루트를 씌운 값입니다.
- 작을수록 좋은 모델입니다.

결정계수(R^2)
- 결정계수(R^2) : 전체 제곱합에서 회귀제곱합의 비율 (SSR / SST)입니다.
- 결정계수가 1에 가까울수록 데이터들이 회귀선 주위에 밀집되어 나타나게 되며 이는 회귀식이 타당하며 설득력이 높다고 볼 수 있습니다.
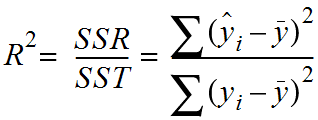
과적합(Overfitting)과 과소 적합(Underfitting)
- 과적합이란 모델이 훈련 데이터의 성질에만 과도하게 학습되어 테스트 데이터에서 오차가 커지는 현상을 말합니다
- 과소 적합이란 과적합도 아니고, 그렇다고 예측을 잘하는 것도 아닌 이도 저도 아닌 훈련/테스트 데이터 모두 오차가 크게 나오는 상황을 말합니다.

편향과 분산의 상충관계( Bias-Variance Trade-off )
- 편향은 점추 정이며, 예측값과 실제값의 차이입니다.
- 즉 모델 학습 시 예측값의 범위가 정답과 얼마나 멀리 있는지를 측정하는 것입니다.
편향이 작다면, 트레인 데이터를 과다 반영 (Overfitting) / 편향이 크다면 트레인 데이터를 최소 반영 (Underfitting)
- 분산은 Test 데이터로, 모델을 검증할 때 발생한 변화
분산이 작으면, Test 데이터로 예측해도, 기존 학습시킨 Train 데이터와 오차가 비슷하다(오차는 많지만), 즉 작은 변동을 뜻합니다. 그러나 분산이 크다면 Test 데이터로 예측하면 큰 오차 발생 ( Overfitting )

편향이 작고, 분산이 작은 모델이 이상적인 모델이다.
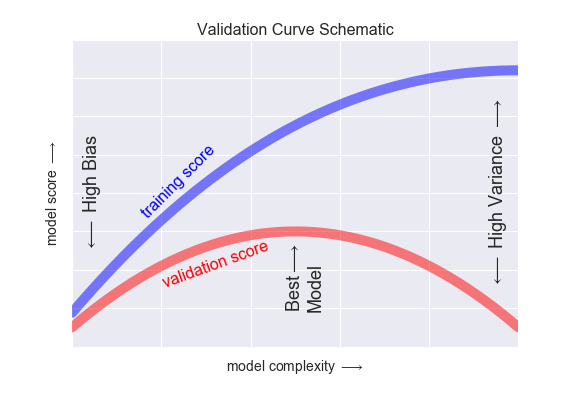
- 하지만 상충 관계이기 때문에, 모델의 복잡도가 높으면 Bias가 증가하고, Variance가 감소하며
- 모델의 복잡도가 낮다면 Bias는 감소하고 Variance가 증가합니다.
- 즉 Bias와 Variance가 최소화되는 정도를 찾아서 모델의 복잡도를 선택하는 게 최선입니다.


- 즉 모델이 복잡해질 수록 훈련 데이터에 맞게, 피팅되어 성능은 증가하지만 검증 데이터의 성능은 어느 정도 증가하다가 오히려 낮아지는 경우를 볼 수 있습니다.
- 즉 과적합이 일어나는 시점이며 복잡한 모델이 필요하지 않다는 것을 알게 됩니다.
다항회귀모델
- 독립변수와 종속변수의 비선형 관계를 학습할 수 있는 모델입니다.
- 즉, 독립변수의 차수를 높여 직선을 곡선으로 만드는 것이며, 단순 선형 모델의 어느 정도 극복할 수 있습니다

- 하지만 너무 차수를 높이게 되면 과적합이 될 수 있습니다.

'머신러닝' 카테고리의 다른 글
| 로지스틱 회귀 ( Logistic Regression ) (0) | 2021.08.05 |
|---|---|
| 원핫인코딩, 특성 선택, 릿지 회귀( Ridge Regression ) (0) | 2021.08.04 |
| 단순선형회귀( Simple-Regression ) (0) | 2021.08.02 |
| Clustering (0) | 2021.07.31 |
| High dimensional data, 차원 축소 (0) | 2021.07.31 |