퍼셉트론과 인공신경망

퍼셉트론(Perceptron)이란?

• 프랑크 로젠블라트(Frank Rosenblatt)가 1957년에 제안한 초기 형태의 인공 신경망입니다.
• 인공신경망을 이루는 가장 기본 단위이며 다수의 신호를 입력으로 받아 하나의 신호를 출력합니다.

• 여기서 신호는, 전류가 전선을 타고 전자가 이동하듯 퍼셉트론이 데이터와 가중치들이 연산의 흐름을 만들어 정보를 계속 전달하는 것과 같습니다.

 

퍼셉트론의 종류

• 단순 퍼셉트론 (은닉층이 없는 것)
  • 가장 기본적인 구조의 퍼셉트론
  • 계단함수를 활성화 함수를 사용하는 모델
• 다층 퍼셉트론 (은닉층이 있는 것)
  • 퍼셉트론이 레이어가 겹쳐 있는 상태
  • 매끈한 활성화 함수를 사용하는 네트워크(시그모이드)

 

 

논리게이트

• 단순논리회로 : 단층 퍼셉트론 

  

   
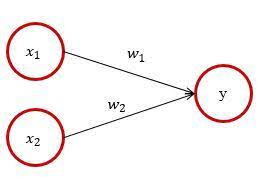
• AND

• def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1*w1 + x2*w2
    if tmp <= theta:
      return 0
    elif tmp > theta:
      return 1
  
  print(AND(0, 0))
  print(AND(1, 0))
  print(AND(0, 1))
  print(AND(1, 1))​

 

• NAND

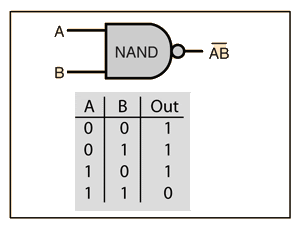
def NAND(x1, x2):
  w1, w2, theta = 0.5, 0.5, 0.7
  tmp = x1*w1 + x2*w2
  if tmp <= theta:
    return 1 ## only change here
  elif tmp > theta:
    return 0 ## only change here

print(NAND(0, 0))
print(NAND(1, 0))
print(NAND(0, 1))
print(NAND(1, 1))​

• OR

 

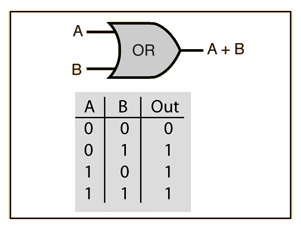
def OR(x1, x2):
  w1, w2, theta = 0.5, 0.5, 0.3 ## only change here
  tmp = x1*w1 + x2*w2
  if tmp <= theta:
    return 0 
  elif tmp > theta:
    return 1

print(OR(0, 0))
print(OR(0, 1))
print(OR(1, 0))
print(OR(1, 1))

 

• 배타적 논리회로 : 퍼셉트론의 한계, "단층 퍼셉트론 으로는 XOR 게이트를 표현할 수 없다". 즉 비선형 영역을 분리할 수 없습니다.

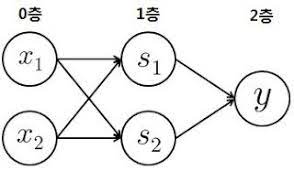
• XOR : 다층 퍼셉트론

• def XOR(x1, x2):
  	s1 = NAND(x1, x2)
      s2 = OR(x1, x2)
      y = and(s1, s2)
      return y
  
  print(XOR(0,0)) # 출력 : 0
  print(XOR(1,0)) # 출력 : 1
  print(XOR(0,1)) # 출력 : 1
  print(XOR(1,1)) # 출력 : 0

  

 

신경망(Neural Networks)

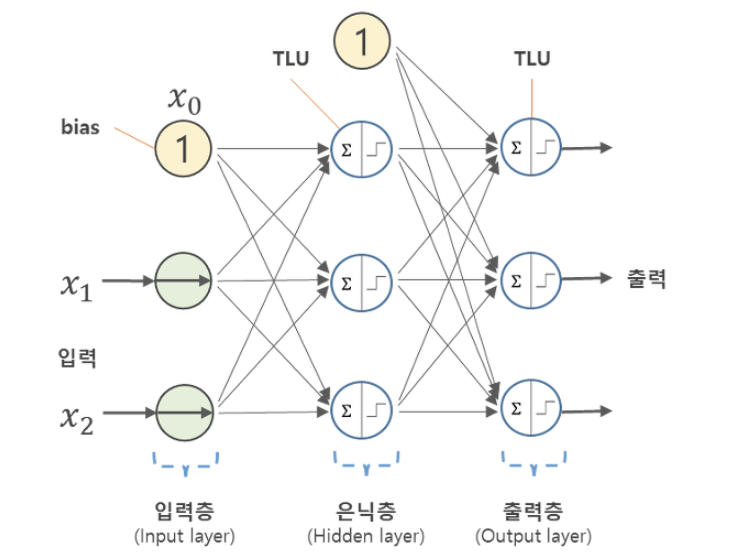
• Artificial Neural Networks(ANN, 인공신경망)이라 불리는 학습모델,
• 뇌의 실제 신경계의 특징을 모사하여 만들어진 계산 모델(computational model)
• 퍼셉트론 알고리즘이 발전하면서 나온 모델이다.
• 기본 구조는 노드들이 엣지로 연결되어 있으면서, 엣지의 가중치를 곱해서 다음 층의 노드로 전달한다
• 입력층 : 입력이 들어노는 계층
• 은닉층 : 입력층과 출력층 사이에 존재하는 것으로, 활성화 함수를 통해 계산하여 임계치를 넘을 경우 다음 노드로 전달한다
• 출력층 : 마지막 은닉층에서 넘어온 값을 활성 함수를 통해 계산하고, 임계 값을 넘는 경우 결과를 출력
  
  • 출력층의 경우 회귀, 분류에 따라 활성화 함수가 나뉩니다.
  • 일반적으로 회귀에는 항등 함수를, 분류에는 소프트 맥스 함수를 사용합니다.
  • 항등함수는 말그대로, 입력을 그대로 출력합니다. 즉 입력과 출력이 항상 같다는 뜻의 항등입니다.
  • 소프트맥스의 경우  출력은 0에서 1.0 사이의 실수로 나타납니다. 또한 출력의 총합은 1입니다. 이덕분에 함수의 출력을
  • '확률'로 해석할 수 있는 것입니다.

 

활성함수(Activation function)

• 임계치(threshold Logic Unit)는 활성함수와 같은 개념으로, 임계치가 만족되면 1로 출력하는 것처럼 활성함수의 조건을 충족하면 다음 노드들이 있는 층(Layer)으로 신호를 전달합니다
• 활성함수는 다양합니다. 계단함수, 시그모이드, ReLU 함수 등이 있습니다. 일단 가볍게 사용 빈도에 대해 설명하자면
• 이론책에는 Sigmoid를 가장 많이 언급하지만, 실제 모델을 생성할때는 ReLU(Rectified Linear Unit) 입니다.
• 출력층에는 대부분 활성함수가 존재하며, 회귀문제의 경우 목표 변수가 실수값인 경우 활성화함수가 필요하지 않지만
• 이진분류, 다중 클래스를 분류하는 경우 시그모이드나, softmax함수를 사용합니다.

 

ReLU 그래프

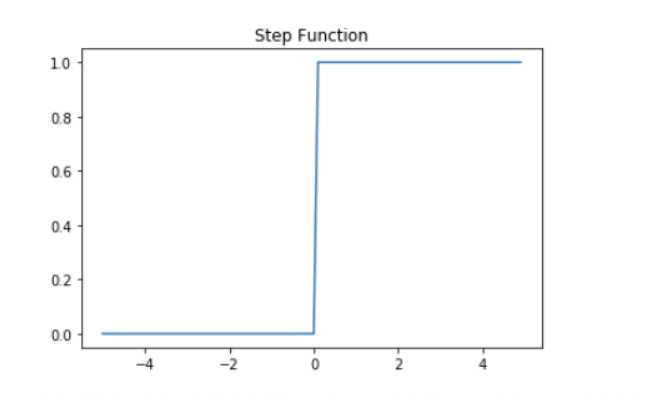
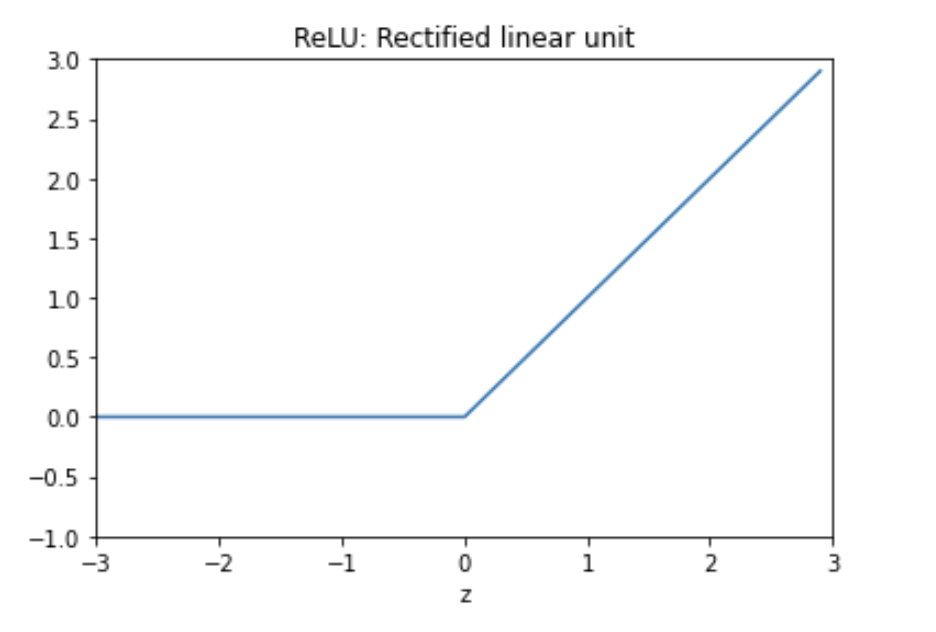
활성함수 처리 과정

 

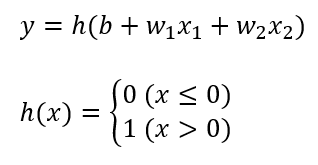
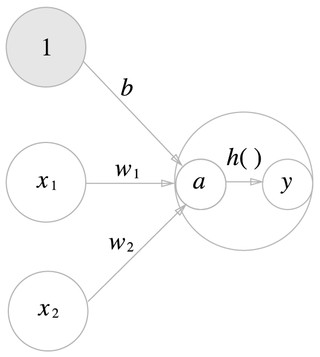
가중치가 달린 입력 신호와 편향의 총합을 계산하고, 이를 a라고 합니다. a를 h( )에 넣어 y를 출력하는 그림입니다.

 

정리

• 인공신경망은 순방향 신경망(feedforward NN)을 학습할 때 손실 함수(Loss function)을 통해 실제값과 예측값의 차이를 평가하고 최소화 하기 위해 경사하강법(Gradient Descent)를  통해 최적의 가중치, bias를 찾는 개념
• 딥러닝 방법론인, 신경망이 강력하다고 하는 이유는 머신러닝 방법론은 일단 유효한 속성에 대해서 분석가가 직접 찾아내야하지만 신경망의 경우 알아서 조합하여 찾아내기 때문에 특성공학(Feature Engineering)을 할필요가 없습니다.
• 특히 Pixel과 같은 고차원의 이미지 데이터를 모델링할 때 알아서 조합하기 때문에 유용합니다.